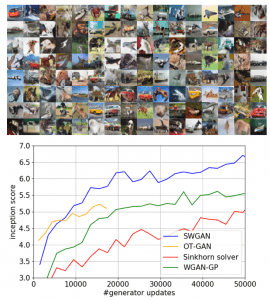Min-max optimization and training generative adversarial networks (GANs): Generative Adversarial Networks (GANs) are one of the most practical methods for learning data distributions. A popular GAN formulation is based on the use of probability distributions such as Wasserstein distance. Unfortunately minimizing such distances is a computationally challenging task. In collaboration with Babak Barazandeh (Splunk), Maziar Sanjabi (Facebook AI), Jason Lee (Princeton), and Jimmy Ba (University of Toronto),we developed a set of tools with theoretical convergence guarantees for training GANs:

• M. Sanjabi, J. Ba, M. Razaviyayn, and J. D. Lee. “On the Convergence and Robustness of Training GANs with Regularized Optimal Transport.” In NeurIPS, 2018, arXiv, GitHub.
• B. Barazandeh, M Razaviyayn, and M. Sanjabi. Training generative networks using random discriminators. In 2019 IEEE Data Science Workshop (pp. 327-332), 2019 (Best Paper Award), arXiv, GitHub.

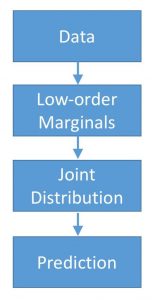
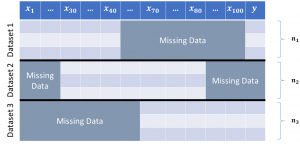Min-max optimization and data imputation:  The ubiquity of missing values in real-world datasets poses a challenge for statistical inference and can prevent similar datasets from being analyzed in the same study, precluding many existing datasets from being used for new analyses. While an extensive collection of packages and algorithms have been developed for data imputation, the overwhelming majority perform poorly if there are many missing values and low sample size, which are unfortunately common characteristics in empirical data. Such low-accuracy estimations adversely affect the performance of downstream statistical models. In collaboration with Sina Baharlouei (USC), Kelechi Ogudu (USC), and Sze-chuan Suen (USC), we develop a statistical inference framework for predicting the target variable without imputing missing values. Our framework led to a computational package RIFLE. Use our package for data imputation and let us know what you think! 

• S. Baharlouei, K. Ogudu, S.C. Suen, and M. Razaviyayn, RIFLE: Robust Inference from Low Order Marginals. arXiv preprint arXiv:2109.00644, 2021, arXiv, GitHub.

---

Nonconvex Smooth Optimization: Stationary Points, Local Optima, and Global Optima

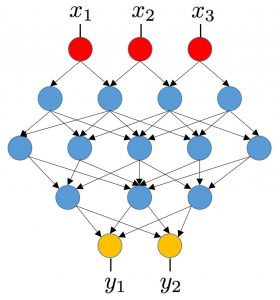Landscape analysis of nonconvex optimization arising in modern deep learning models: Training deep statistical models, such as deep neural networks, is a computationally challenging task. These models map the input (feature) vector to the output (response) vector through the composition of multiple simple mappings. Training feedforward multi-layer neural networks or low-rank matrix decomposition are examples of such a problem. In collaboration with Maher Nouiehed (USC), we developed a mathematical framework for analyzing the local optima of training these deep models. In particular, by leveraging concepts from differential geometry, we provide sufficient conditions under which all local optima of the objective function are globally optimal. Our initial result leads to a simple characterization of the local optima of linear feedforward network and hierarchical non-linear neural networks: 

• M. Nouiehed and M. Razaviyayn. “Learning deep models: Critical points and local openness,” to appear in INFORMS Journal on Optimization, available at  arXiv:1803.02968, 2018.

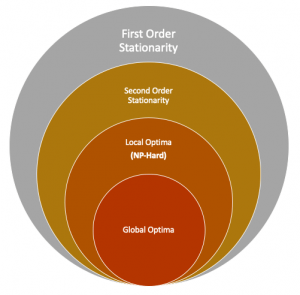Algorithms for escaping spurious stationary points: Many modern practical optimization problems are nonconvex. In such problems, it is crucial for an optimization algorithm to be equipped with modules for escaping spurious saddle points and finding higher-order stationary solutions. In collaboration with Maher Nouiehed (USC), Songtao Lu (IBM AI Research), and Mingyi Hong (University of Minnesota), we consider the problem of finding a local optimum of a constrained non-convex optimization problem. We show that, unlike the unconstrained scenario, the vanilla projected gradient descent algorithm fails to escape saddle points even in the presence of a single linear constraint. We then proposed a series of algorithms for finding second-order stationary points to smooth constrained nonconvex optimization problems. Check our publications:

• M. Nouiehed, J. D. Lee, and M. Razaviyayn. Convergence to second-order stationarity for constrained non-convex optimization. arXiv preprint arXiv:1810.02024.
• M. Nouiehed and M. Razaviyayn. A Trust Region Method for Finding Second-Order Stationarity in Linearly Constrained Nonconvex Optimization. SIAM Journal on Optimization, 30(3), 2501-2529, 2020.
• S. Lu, M. Razaviyayn, B. Yang, K. Huang, M. Hong. Finding second-order stationary points efficiently in smooth nonconvex linearly constrained optimization problems. Advances in Neural Information Processing Systems, 2020 (Spotlight Presentation at NeurIPS 2020).
• S. Lu, J. D. Lee, M. Razaviyayn, and M. Hong. “Linearized ADMM Converges to Second-Order Stationary Points for Non-Convex Problems.” IEEE Transactions on Signal Processing 69 (2021): 4859-4874.
• M. Hong, M. Razaviyayn, and J. Lee. “Gradient primal-dual algorithm converges to second-order stationary solution for nonconvex distributed optimization over networks.” In International Conference on Machine Learning, pp. 2009-2018. PMLR, 2018.

---

Federated Learning and Distributed Optimization:

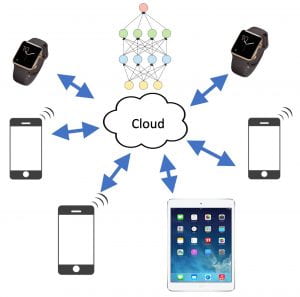Federated learning (FL) is a distributed learning paradigm in which many clients with heterogeneous data, collaborate to learn a model. Distributed optimization framework is key in such FL settings. In a series of works and in collaboration with Andrew Lowy (USC), Songtao Lu (IBM AI Research), Mingyi Hong and Zhi-Quan Luo (University of Minnesota), and Jason Lee (Princeton University), we developed efficient distributed algorithms that can escape saddle points and converge to higher-order stationary solutions. In addition, we studied the FL setting in the presence of sensitive data using Local Differential Privacy (LDP). LDP provides a strong guarantee that each client’s data cannot be leaked during and after training, without relying on a trusted third party. Our works can be found at:

• A. Lowy and M. Razaviyayn. “Locally Differentially Private Federated Learning: Efficient Algorithms with Tight Risk Bounds.” arXiv preprint arXiv:2106.09779, 2021.
• M. Hong, M. Razaviyayn, and J. D. Lee. “Gradient primal-dual algorithm converges to second-order stationary solution for nonconvex distributed optimization over networks.” In International Conference on Machine Learning, pp. 2009-2018. PMLR, 2018.
• M. Hong, Z.-Q. Luo, and M. Razaviyayn. “Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems.” SIAM Journal on Optimization 26, no. 1: 337-364, 2016.

---

Variance Amplification of First-Order Methods

---

Past Research: Optimal Generalizability in Parametric Learning

Joint work with Ahmad Beirami (Facebook Research), Shahin Shahrampour (Texas A&M University), and Vahid Tarokh (Duke University)

We consider the parametric learning problem, where the objective of the learner is determined by a parametric loss function. Employing empirical risk minimization with possible regularization, the inferred parameter vector will be biased toward the training samples. Such bias is measured by the cross-validation procedure in practice where the data set is partitioned into a training set used for training and a validation set, which is not used in training and is left to measure the out-of-sample performance. A classical cross-validation strategy is the leave-one-out cross-validation (LOOCV) where one sample is left out for validation and training is done on the rest of the samples that are presented to the learner, and this process is repeated on all of the samples. Despite simplicity and efficiency, this method is rarely used in practice due to the high computational complexity. In this work, we first derive a computationally efficient estimator of the LOOCV and provide theoretical guarantees for the performance of the estimator. Then we use this estimator to develop an optimization algorithm for finding the optimal regularizer in the empirical risk minimization framework. In our numerical experiments, we illustrate the accuracy and efficiency of the LOOCV estimator as well as our proposed algorithm for finding the optimal regularizer.

---

Past Research: De novo Transcriptome Error Correction by Convexification

Joint work with Sina Baharlouei (University of Southern California), Elizabeth Tseng (Pacific Biosciences), and David Tse (Stanford University)

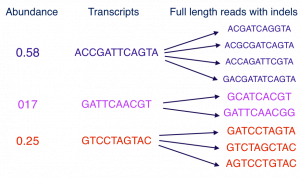
De novo transcriptome recovery from long sequencing reads is an essential task in computational biology. Mathematically, this problem is a huge dimensional clustering problem over a discrete space. By exploiting this discrete structure, we propose a parallel algorithm for joint error correction and abundance estimation. Unlike the existing software package TOFU, which has quadratic computational complexity, the computational complexity of our proposed algorithm scales linearly with the number of reads. Moreover, our initial numerical experiments show improvement over the existing software packages in terms of the number of denoised reads. See our work here and our computational package GitHub repository.

---

Past Research: Inference and Feature Selection Based on Low Order Marginals

Joint work with: Farzan Farnia (Stanford University), Sreeram Kannan (University of Washington), and David Tse (Stanford University)

Abstract. Consider the classification problem of predicting a target variable Y from a discrete feature vector X = (X1,…, Xd). In many applications, estimating the joint distribution P(X, Y) is computationally and statistically impossible for large values of d. Therefore, an alternative approach is to first estimate some low order marginals of the joint probability distribution P(X, Y) and then design the classifier based on the estimated low order marginals. This approach is also helpful when the complete training data instances are not available due to privacy concerns. For this inference problem, we introduced the “minimum Hirschfeld-Gebelein-R’enyi (HGR) correlation principle” and proved that for a given set of marginals, this principle leads to a randomized classification rule which is shown to have a misclassification rate no larger than twice the misclassification rate of the optimal classifier. We numerically compare our proposed algorithm with the DCC classifier and show that the proposed algorithm results in a better misclassification rate over various UCI data repository datasets.

---

Past Research: Personalized Disease Prediction Using Multi-Omics Data

Joint work with: Farzan Farnia, Jinye Zhang, and David Tse (Electrical Engineering, Stanford University), Rui Chen, Tejas Mishra, and Michael Snyder (Genetics, Stanford University)

Abstract. The advances in high throughput sequencing technologies and sensors collecting health data made a massive amount of health data accessible to each individual. Personalized medicine takes the advantage of this massive data for medical risk assessment, prediction, diagnosis, and treatment of disease based on each individual’s specific genetic composition and health records. The goal of this project is to predict disease states based on multi-omics profiles of hundred individuals with the collected data size being over petabytes for individuals. This high-dimensional problem has the following main challenges. First, similar to any other high-dimensional settings, special consideration should be given to overfitting and false discoveries. Second, the variations between the omics profile of individuals in the healthy states are much larger than the variations between the healthy and disease states within any given individual. Third, in order to select interpretable features, the original feature variables should be mapped to the well-studied biological pathways. Using sparse graphical lasso and permutation test, we developed a testing procedure for discovering pathways with significant expression level change in the disease and healthy states. Moreover, theoretically, we have shown that the simple sign test is maximin in the one-sided case and near maximin in the two-sided case over for the class of Gaussian distributions.

---

Past Research: Successive Upper-bound Minimization Strategies for Large Scale Optimization

Joint work with: Mingyi Hong (Iowa State University), Maziar Sanjabi (University of Minnesota), Tom Luo (University of Minnesota), Jong-Shi Pang (University of Southern California)

Abstract. The block coordinate descent (BCD) method is widely used for minimizing a continuous function f of several block variables. At each iteration of this method, a single block of variables is optimized, while the remaining variables are held fixed. To ensure the convergence of the BCD method, the subproblem of each block variable needs to be solved to its unique global optimal. Unfortunately, this requirement is often too restrictive for many practical scenarios. In this series of works, we first study an alternative inexact BCD approach that updates the variable blocks by successively minimizing a sequence of approximations of f which are either locally tight upper bounds of f or strictly convex local approximations of f. Different block selection rules are considered such as cyclic (Gauss-Seidel), greedy (Gauss-Southwell), randomized, or even multiple (Parallel) simultaneous blocks. We characterize the convergence conditions and iteration complexity bounds for a fairly wide class of such methods, especially for the cases where the objective functions are either non-differentiable or non-convex. Also the case of existence of a linear constraint is studied briefly using the alternating direction method of multipliers (ADMM) idea. In addition to the deterministic case, the problem of minimizing the expected value of a cost function parameterized by a random variable is also investigated. An inexact sample average approximation (SAA) method, which is developed based on the successive convex approximation idea, is proposed and its convergence is studied. Our analysis unifies and extends the existing convergence results for many classical algorithms such as the BCD method, the difference of convex functions (DC) method, the expectation-maximization (EM) algorithm, as well as the classical stochastic (sub-)gradient (SG) method for the nonsmooth nonconvex optimization, all of which are popular for large scale optimization problems involving big data. Two of our papers were among the Finalists of the Best Paper Prize for Young Researcher in Continuous Optimization in ICCOPT 2013 and ICCOPT 2016.

---

Past Research:  Interference Management in Wireless Heterogeneous Networks

Joint work with: Hadi Baligh (Huawei Technologies), Mingyi Hong (Iowa State University) , Wei-Cheng Liao (University of Minnesota), Gennady Lyubeznik (University of Minnesota), Tom Luo (University of Minnesota), Maziar Sanjabi (University of Minnesota), and Ruoyu Sun (University of Minnesota)

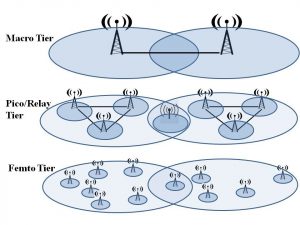
Abstract. The design of future wireless cellular networks is on the verge of a major paradigm change. With the proliferation of multimedia-rich services as well as smart mobile devices, the demand for wireless data has been increased explosively in recent years. In order to accommodate the explosive demand for wireless data, the cell size of cellular networks is shrinking by deploying more transmitters such as macro, micro, pico, femto base stations, and relays. These nodes utilize the same frequency bands and are densely deployed to provide coverage extension for cell edge and indoor users. Deploying more transmitters brings the transmitters and receivers closer to each other, thus we are able to provide high link quality with low transmission power. Unfortunately, the close proximity of many transmitters and receivers introduces substantial intracell and intercell interference, which, if not properly managed, can significantly affect the system performance. The key challenge for interference management in the new wireless networks is to develop low-complexity schemes that mitigate the multiuser interference in the system, optimally balance the overall spectrum efficiency and user fairness. This chapter deals with various theoretical and practical aspects of interference management for multi-user cellular networks. In particular, we study the interference management in the physical and MAC layer using optimized beamforming and scheduling techniques. We utilize the successive convex approximation idea to develop algorithms for this purpose. Our work here won the Signal Processing Society Young Author Best Paper Award in 2014.

---

Past Research: Dictionary Learning for Sparse Representation: Complexity and Algorithms

Joint work with: Andy Tseng (University of Minnesota) and Tom Luo (University of Minnesota)

Abstract. We consider the classical dictionary learning problem for sparse representation in machine learning literature. We first show that this problem is NP-hard based on the polynomial time reduction of the densest cut problem in a graph. Then we propose an efficient dictionary learning scheme to solve several practical formulations of this problem to a stationary point. Unlike many existing algorithms in the literature, such as K-SVD, our proposed dictionary learning scheme is theoretically guaranteed to converge to the set of stationary points under certain mild assumptions. For the image denoising application, the performance and the efficiency of the proposed dictionary learning scheme are comparable to that of K-SVD algorithm in the simulation.