Skip to content

Multi-channel computational electromagnetics

We need full-wave solutions of Maxwell’s equations to make quantitative predictions about the wave propagation and scattering in complex multi-channel optical systems such as disordered media, aperiodic metasurfaces, channel [de]multiplexers, and photonic circuits. However, these simulations are often prohibitively slow, given the multiple length scales and the large number of input channels (independent angles, spatial spots, or waveguide modes) involved. Each input channel requires the solution of one distinct scattering problem. Our group develops methods to overcome this computational bottleneck.

Conventional methods to solve Maxwell’s equations numerically discretize the system on a basis and then solve for all the unknowns in this basis set. However, such a basis may contain millions to billions of elements, while we only need to extract a relatively small number of data points from it (e.g., the amplitude of light scattered to the directions or waveguide modes of interest). An additional loop over the many input channels exacerbates the inefficiency of a full-basis solution, as illustrated in the schematic below.

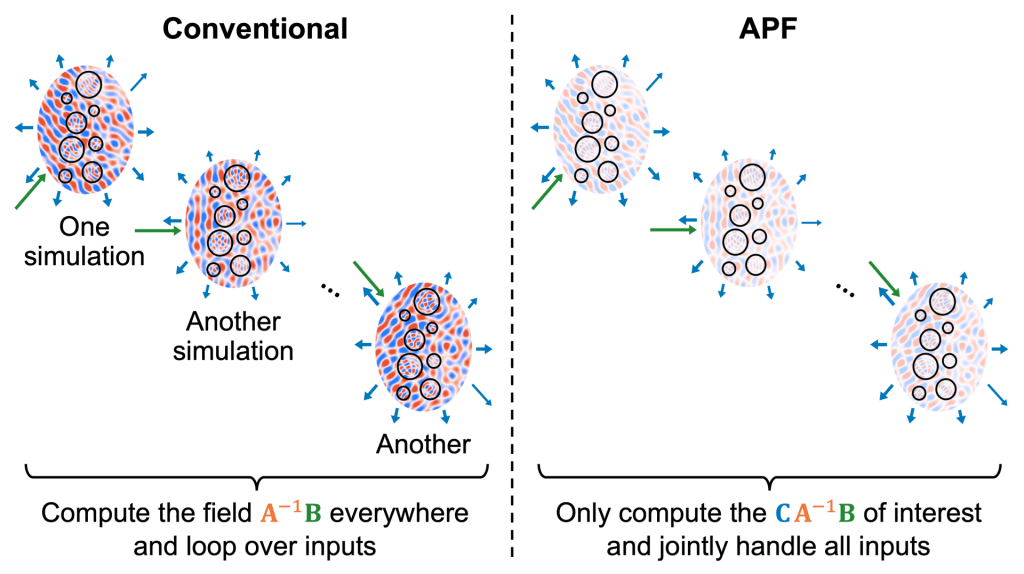
Concept of augmented partial factorization (APF).

We came up with a more efficient strategy that computes only the quantities of interest. Any response properties in the linear regime can be encapsulated in a generalized scattering matrix CA-1B where A discretizes the Maxwell differential operator, the columns of matrix B contain different input source profiles of interest, and the rows of matrix C contain different output projection profiles of interest. Instead of evaluating the full-basis solution X = A-1B, we directly compute the orders-of-magnitude-smaller projected matrix CA-1B through a partial LU factorization of an augmented matrix K = [[A, B]; [C, 0]] as shown in the figure below. Doing so eliminates the many full-basis solutions A-1B from the augmented linear system without solving for them. This approach, which we call “augmented partial factorization” (APF) [1], is well suited for multi-channel problems since it jointly handles the many inputs without a loop over them. It is exact and applicable to any discretization scheme in any dimension.

The augmented matrix K = [[A, B]; [C, 0]] and its partial factorization in APF.

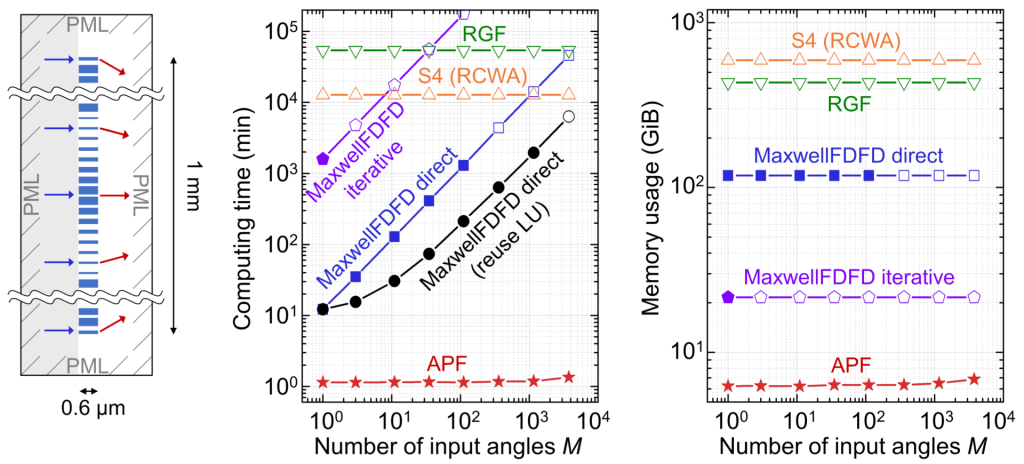
For massively multi-channel problems, APF can reduce computing time by many orders of magnitude while lowering memory usage (see figure below) without compromising accuracy [1]. This drastic speed-up enabled us to perform full-wave simulations of scattering matrix tomography and other imaging methods [2], demonstrate the enhanced backscattering correlations for entangled photon pairs scattered from disorder [3], and validate the existence of perfectly transmitting wavefronts through strong disorder in 3D [4].

Benchmark of augmented partial factorization (APF) and other methods on a mm-wide metasurface in 2D.
Incident-angle dependence of a hyperbolic metalens computed with APF.

We also developed multi-channel gradient computation using APF and used it for the inverse design of aperiodic metasurfaces [5], as shown below for a broad-angle beam splitter.

A broad-angle metasurface beamsplitter designed with APF.

We developed an open-source software called MESTI (Maxwell’s Equations Solver with Thousands of Inputs) written in Julia [6] and MATLAB [7] that implements both APF and the conventional direct method. MESTI uses finite-difference discretization on the Yee grid. It supports any dimension, any tensor relative permittivity profile, any set of input source profiles, any set of output projection profiles, and comes with PML and the common boundary conditions. Multithreading and MPI are supported via the MUMPS sparse linear solver package. We also wrote a tutorial on using APF and the MESTI software to carry out wavefront shaping simulations [8].

Related publications

  1. Fast multi-source nanophotonic simulations using augmented partial factorization, Ho-Chun Lin, Zeyu Wang, and Chia Wei Hsu. Nature Computational Science 2, 815–822 (2022).
  2. Full-wave simulations of tomographic optical imaging inside scattering media, Zeyu Wang, Yiwen Zhang, and Chia Wei Hsu. arXiv:2308.07244.
  3. Coherent backscattering of entangled photon pairs, Mamoon Safadi, Ohad Lib, Ho-Chun Lin, Chia Wei Hsu, Arthur Goetschy, and Yaron Bromberg. Nature Physics 19, 562–568 (2023).
  4. Full transmission of vectorial waves through 3D multiple-scattering media, Ho-Chun Lin and Chia Wei Hsu. arXiv:2406.06727.
  5. Fast multichannel inverse design through augmented partial factorization, Shiyu Li, Ho-Chun Lin, and Chia Wei Hsu. ACS Photonics 11, 378–384 (2024).
  6. github.com/complexphoton/MESTI.jl
  7. github.com/complexphoton/MESTI.m
  8. Wavefront shaping simulations with augmented partial factorization, Ho-Chun Lin, Zeyu Wang, and Chia Wei Hsu. arXiv:2406.09342.
University of Southern California