Hermitian operators describe physical observables in a closed quantum system. But in optics, non-Hermiticity arises through optical gain and loss that amplifies and dissipates light. At the degeneracy of a non-Hermitian system, two eigenstates coalesce into one at an “exceptional point,” giving rise to fascinating and counter-intuitive properties. Meanwhile, the nonlinearity in a material’s optical response enables frequency generation and light-light interactions. At our group, we are interested in the interplay between non-Hermiticity and nonlinearity.
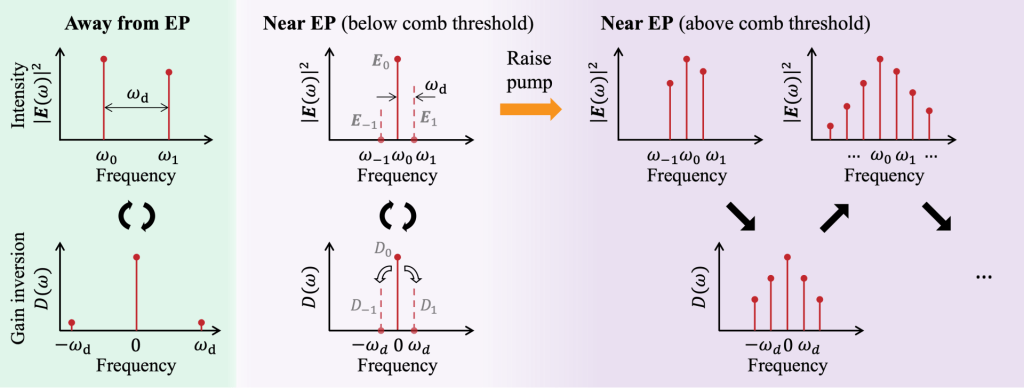
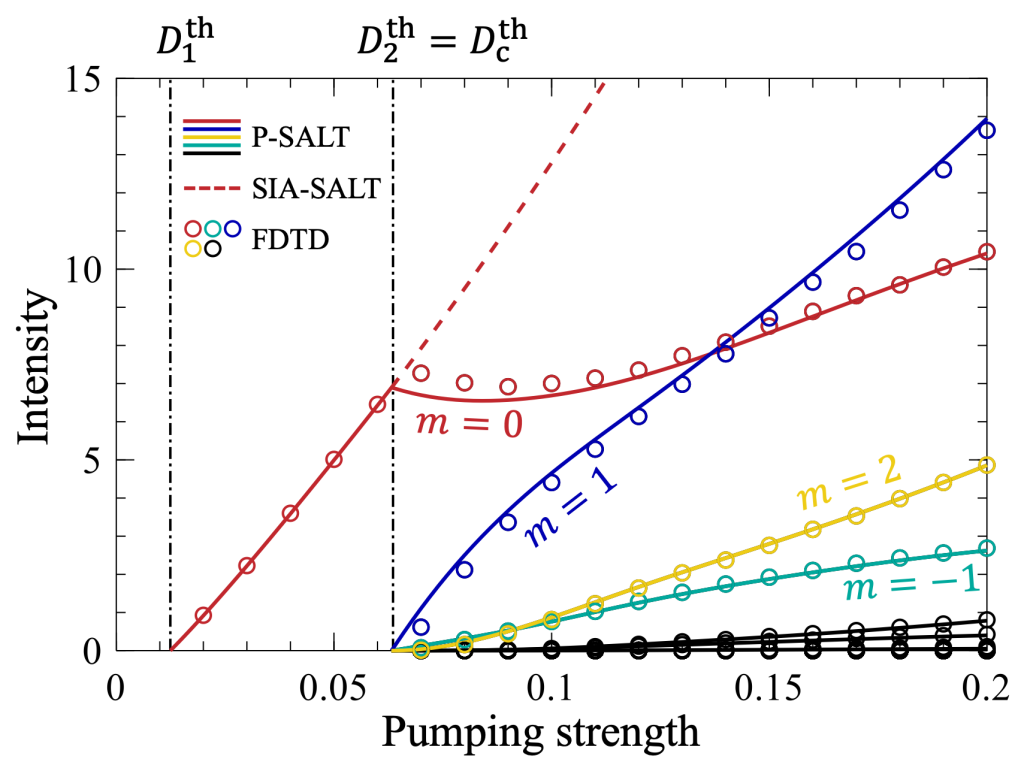
The optical gain in lasers is capable of extreme nonlinearity and is intrinsically non-Hermitian. We explore what a nonlinear gain can do beyond amplifying light. To build the toolkit for such studies, we developed an exact solution of the space-dependent Maxwell–Bloch equations with a dynamic population inversion, which we call “periodic-inversion steady-state ab initio laser theory” (P-SALT) [1]. With this theory, we predicted that when a laser comes sufficiently close to an exceptional point, the beating between two lasing modes will drive the gain inversion to oscillate in time, and the oscillating gain enables four-wave mixing to generate new frequencies and create a frequency comb (illustrated in the figure below). The comb formation involves a multi-spectral multi-modal instability, markedly different from how a conventional laser works. The resulting frequency comb exhibits many unique properties, including an ultra-compact size, a tunable repetition rate, and a self-starting operation—all promising for future applications. This is an example of how non-Hermiticity and nonlinearity can work together to fundamentally change the behavior of an optical system.
Related publications
- Dynamic gain and frequency comb formation in exceptional-point lasers, Xingwei Gao, Hao He, Scott Sobolewski, Alexander Cerjan, and Chia Wei Hsu. arXiv:2310.14643.