Interplay of instabilities and effective states of stress. Can a material instability at the microscopic scale suppress a structural instability at the engineering scale? We have studied this question systematically in the context of nematic elastomer sheets.
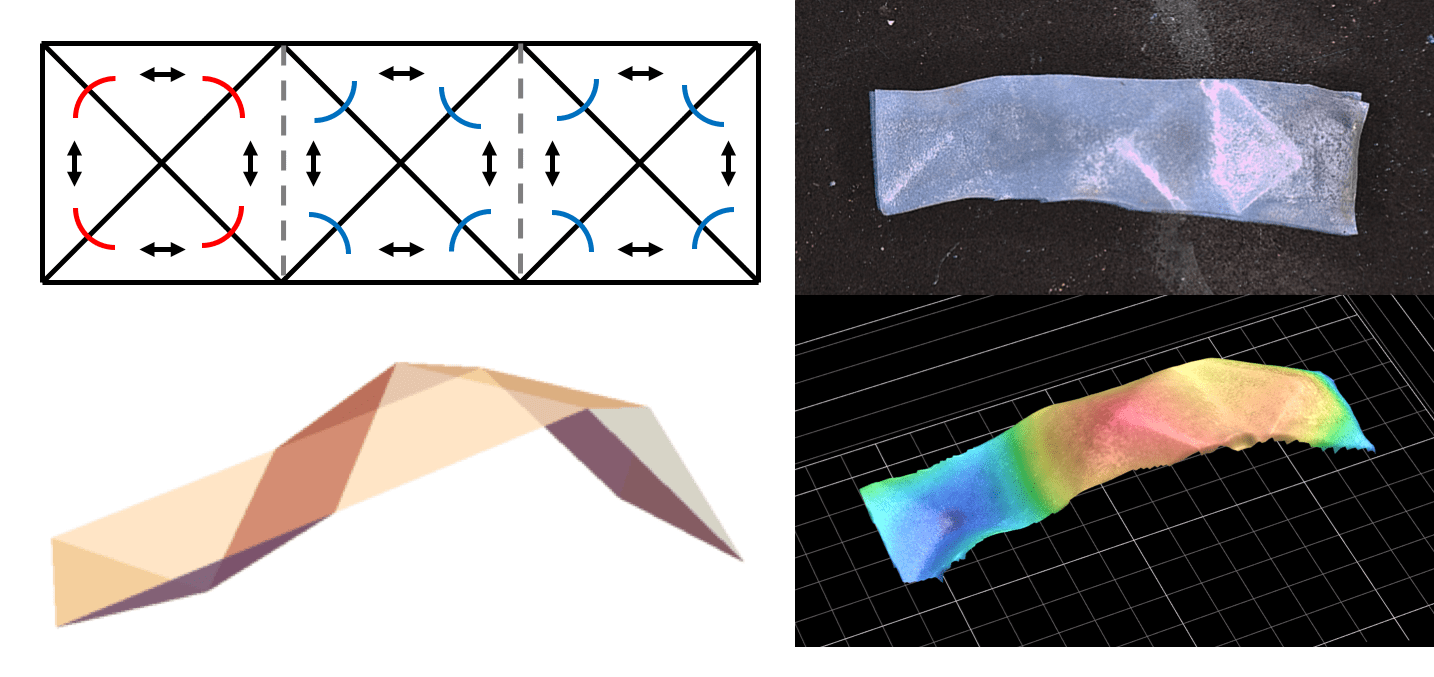
The clamped-stretch experiment of Kundler and Finkelmann.
Nematic elastomers are composed of rigid rod-like liquid crystal molecules pendent to a soft polymer network. The liquid crystals tend to align at low temperature, with the average alignment at each point in a continuum sample described by a unit vector called the director field. These elastomers deform anisotropically due to this alignment; essentially, the soft polymer network wants to stretch along and contract transverse to this director field. At the same time, the director field wants to reorient to align with the maximum stretch of the deformation. This interplay gives rise to a nematic elastic coupling that enables unique mechanical properties such as soft elasticity and fine-scale microstructure. For instance, a thin mono-domain nematic elastomer, which is clamped and stretched transverse to the initial alignment of the director field, forms fine-scale stripe domains of oscillating nematic director (i.e.,“microstructure”) to accommodate deformation — the cloudy regions depicted above. Interestingly, this thin clamped stretched nematic elastomer sheet does not wrinkle, even though wrinkling is pervasive in thin sheets of normal elastomer under this boundary condition. This motivated our investigation.
Through rigorous analysis and numerical modeling, we showed that taut and appreciably stretched sheets of nematic elastomer are capable of suppressing wrinkling by modifying the effective state of stress through the formation of microstructure. The key insight is the unusual effective state of stress exhibited by this strip-domain microstructure. The material can macroscopically shear without shear stress for a certain range of deformation, and this unusual stress state appears precisely at the clamps (top-right in the figure) under the clamped-stretched boundary condition. Conventional materials, on the other hand, have a tendency to produce slight compressive stress just ahead of the clamps prior to the onset of wrinkling. With the absence of this compressive stress, there is no reason for the material to wrinkling.
Thus, we have learned that a material instability can produce a novel effective state of stress (shear strain without shear stress), which can, in turn, suppress a structural instability (wrinkling). Building on these ideas, we aim to leverage advances in manufacturing and materials development to tailor material instabilities to produce desirable engineering-scale stress states. Sheets with architectured cuts (kiragami) are a particularly interesting template with which to pursue these ideas. While much is know on their behavior as mechanisms (the stress-free states), much is left to explore when these systems are stressed.
Active, objective and reconfigurable origami. The seamless integration of function and form promises to spur innovation in technologies ranging from MEMS and NEMS devices (e.g., with novel electrical, electromagnetic and energy functionality), reconfigurable robotics, wearable electronics and compliant bio-medical devices. For surfaces, we see origami as the most promising “form” to enable function. Indeed, Gauss’s Theorema Egregium (Remarkable Theorem) informs us that a sheet cannot bend in two directions without incurring some form of stretch. This is why one sees localization and crumpling when compressing a piece of paper into a ball. In origami, we take advantage of this fact by exploiting this localization in the careful design of crease patterns.
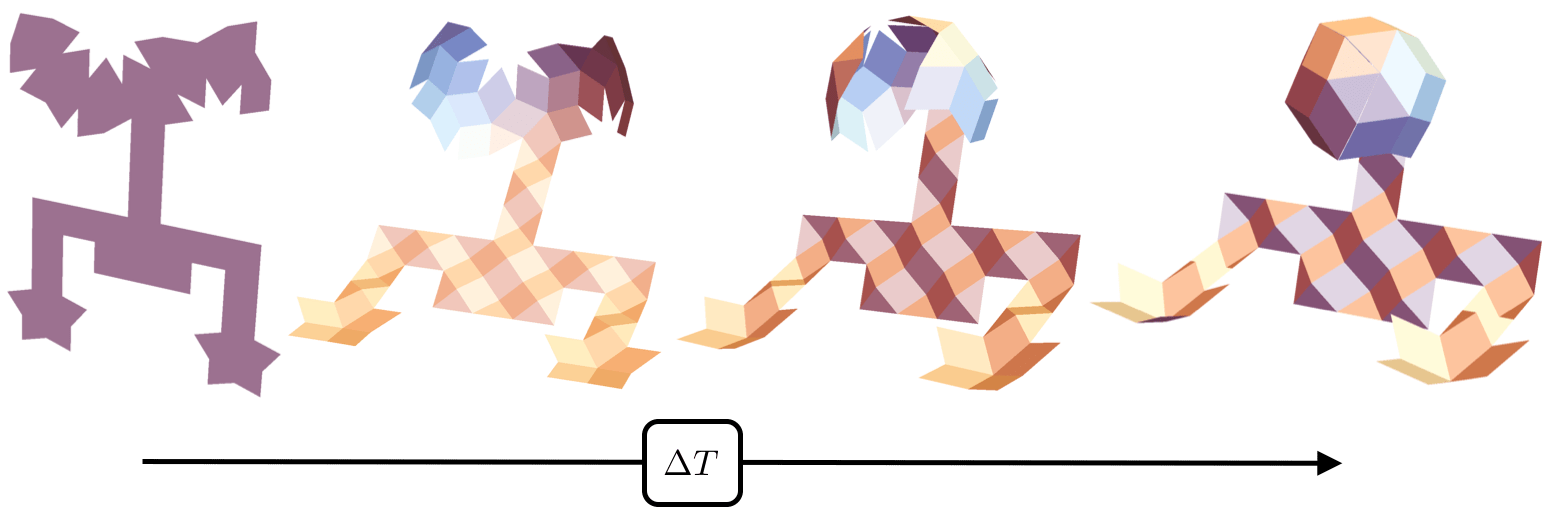
Active Origami. It is difficult to fabricate complex three dimensional morphologies. Alternatively, through patterning active (initially flat) sheets, complex three dimensional shapes can be realized upon external stimuli. For example, the nematic elastomer sheet below has been patterned to attain an actuation involving two pyramids going up and one going down. By composing together simple building blocks like this, it is possible to design very complex shape such as the “soft robot” (also below). Future directions include collaborating with experimentalist to integrate this design framework with (the more robust) 3D/4D printed nematic elastomer systems. These 3D/4D printed systems also raise interesting theoretical questions; for instance, how does one describe an appropriate “sheet” theory for such systems, i.e., one that is rooted in the underlying physics? This is, additionally, a direction we aim to explore.
Design, predicted actuation, and experimental realization of nonisometric origami.
Complex shape from simple building blocks.
Objective origami. An objective origami is a structure composed of unit cells where corresponding points within each unit cell see the same environment. The cylindrical origami below are examples. Notice that these structure are mulit-stable. That is, by suitable mechanical loading, each of the two structures below can transform from one of the stated depicted to another. This results in dramatic twist and contraction (or extension) of the overall structure. We aim to classify all objective origami and study their properties, as many of these structures can be technological interest: For instance, multi-stable tubes can be integrated in the design of medical stents. These require a closed state (small diameter) for deployment and an open state (large diameter) to direct the blood-flow once deployed — a feature which can be exhibited and characterized systematically in objective origami.
Multi-stable cylindrical origami.
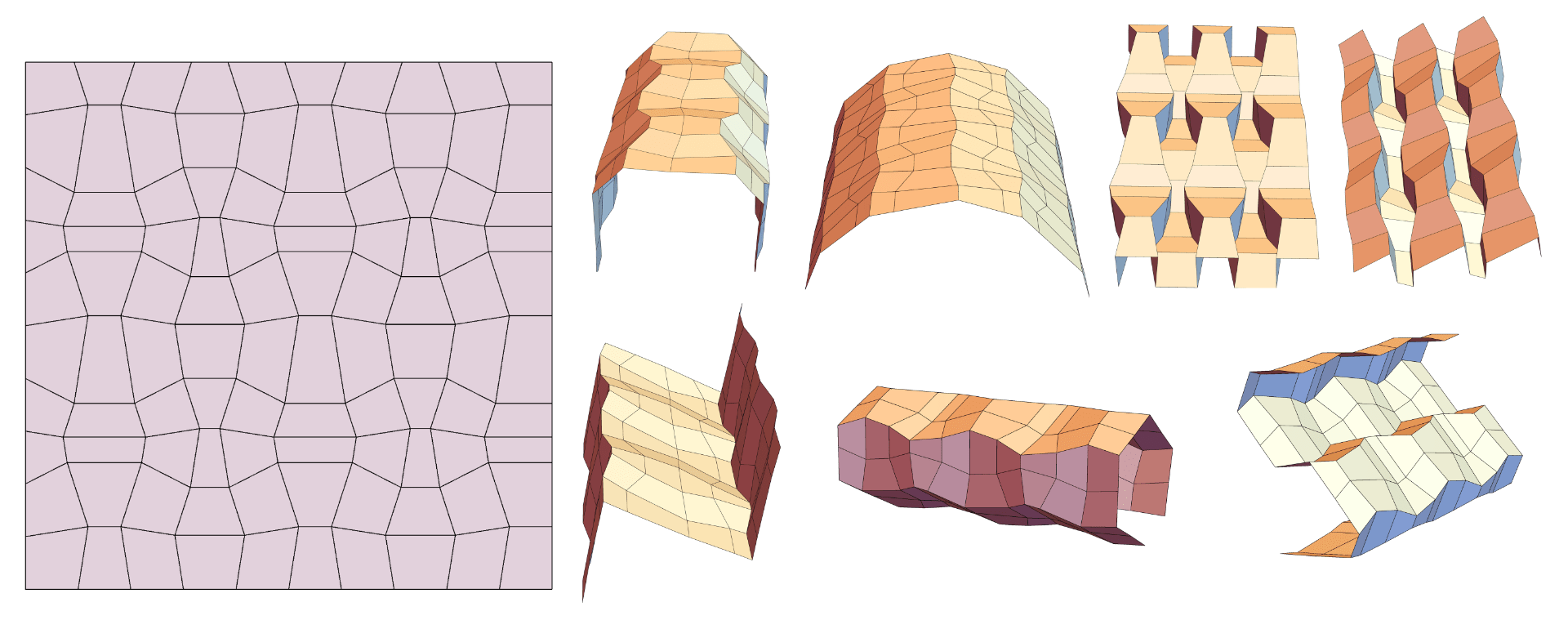
Reconfigurable origami. The classical and well-known Miura origami pattern is capable of deforming from flat to folded flat without any stretch in the tiles. It turns out that there are many other crease patterns with similar reconfigurability capability. We have recently developed a fairly complete description of their designs and kinematics, and this lead to a fast algorithm that parameterizes the entire configuration space. An interesting example of reconfigurable origami enabled by our analysis is given below. This particular crease pattern can be folded from flat to folded flat in over 1000 unique ways. We highlight seven intermediate configurations achieved by folding along different mountain-valley assignments. In the future, we aim to take the developed algorithm and incorporate it into an optimization scheme to attack the inverse problem: Given an arbitrary surface, find a rigidly and flat foldable origami which approximately resembles the surface. If successful, this “closing-of-the-loop” will provide designers with a powerful tool to explore the configuration space of reconfigurable structures.
Highly reconfigurable origami.
Shape memory alloys and helical nano-structures. We are a curiosity-driven research group looking to provide fundamental insights to striking phenomenon found in physics, material science and engineering. This has lead us to pursue lines of research on a broad range of topics.
In bulk crystalline solids, it is well-known that the presence of compatible interfaces at microscopic scales is related to the lattice parameters describing the periodicity of their crystalline phases. This is exemplified, for instance, in the CuAlNi sample displayed below. The high symmetry austenite phase and the low symmetry martensite phase are not kinematically compatible at an interface. Thus, on cooling below a critical temperature, the martensite phase nucleates as fine-scale twins to accommodate — in the sense of averages — that parent austenite phase at a habit plane. These twins often branch into finer and finer twins as they approach the interface. We have developed a model to realistically capture the length scales and energy of this characteristic microstructure. The left image is a simulation of the model consistent with the experimental parameters of the CuAlNi sample to the right.
This characteristic microstructure cost significant energy when the shape memory alloy undergoes phase transformation. But what if these features are not needed; that is, what if the austenite is directly compatible with the martensite? Recent efforts in the tuning of lattice parameters to achieve such compatibility of phases have lead to remarkable macroscopic properties, including near-zero thermal hysteresis for such solids undergoing phase transformation. But the tuning is never perfect; in ideality, the requirement is a set of formulas that in practice is only ever satisfied approximately. Thus, a future research direction is to adapt our modeling efforts to the setting of tuned parameters, with the hope of gaining insight into approximate satisfaction of the conditions.
The CuAlNi sample of C. Chu (right), and our modeling of the phenomenon (left).
As the results above indicate, symmetry and the presence of compatible interfaces at microscopic scales play an important role in the functionality of bulk crystalline solids. One thus wonders if this line of thinking be applied more generally? The structure of matter in many examples—in, for instance, nanoscience and biology—is that of discrete symmetries that are not inherently periodic: single wall carbon nanotubes of any chirality, BCN, GaN, MoS2, WS2, non-animal viruses such as the tail sheath of bacteriophage T4, bacterial flagella, microtubules, . . . , to name a few. These are helical structures.
We systematically studied phase transformations from one helical structure to another and provided necessary and sufficient conditions on the structural parameters of the two helical phases such that they are compatible. We showed that there are three (and only three) types of compatible interfaces that fix the axis of the helical structure: vertical, horizontal and helical interfaces—each named for the physical appearance on the structure. Examples of compatible helical and horizontal interfaces are given below. These results provide a basis for the tuning of helical structural parameters so as to achieve compatibility of phases. In forthcoming works, we will apply this theory to interesting special cases, especially to guide the design of structure-dependent tension-twist protocols that can induce specific phase transformations.
Helical and horizontal interfaces in nanotubes.